公式自体の証明は後ほど)。 応用公式1の証明 「放物線の式」ー「直線の式」= a ( x − α) ( x − β) a (x\alpha) (x\beta) a(x− α)(x −β) と表せるので,放物線と直線で囲まれた部分の面積は, S = ∣ ∫ α β a ( x − α) ( x − β) d x ∣ S=\left\displaystyle\int_ {\alphaヘロンの公式公式ヘロンの公式 3辺の長さがそれぞれ, , であるような三角形の面積は次の式で求まる但し, とする ヘロンの公式は, 三角形の3辺の長さが分かっているときにその面積を求めるための公式です 実際に計算してみると分かるのですが, 3辺の長さがすべて有理数の場合は計算が楽面積分 ベクトル解析 における 面積分 (めんせきぶん、 surface integral )は、 曲面 上でとった 定積分 であり、 二重積分 として捉えることもできる。 線積分 は一次元の類似物にあたる。 曲面が与えられたとき、その上の スカラー場 や ベクトル場 を
平行四边形的面积公式是什么
面積公式
面積公式- ひし形の面積の公式は 「たての対角線の半分の長さ」と「横の対角線の半分の長さ」の直角三角形の 4倍 と考えると分かりやすいです。 「たての対角線の半分の長さ」と「横の対角線の半分の長さ」の直角三角形の面積は \(高さ×底辺÷2=(たて÷2)×(横÷2)÷2\)三角形の面積を求めるためには 一旦、平行四辺形の面積を求め それを半分にしている。 だから、2で割る必要があるんですね! 忘れないように覚えておきましょう(^^) 三角形の面積を求める問題 それでは、三角形の面積公式を使って問題を解いていき



三角锥形面积公式三角形的体积公式是什么 银颜网
既習の面積公式をもとに,三角形や平行四辺形などの面積を求める公式を進んで見出そうとしている。 数学的な考え方 既習の面積公式をもとに,三角形や平行四辺形などの面積を工夫して求めたり,公式をつくることができる。 技 能土地の面積を変えないため、2.で求めた面積を用いて、次の式を組み立てる。 ここで、1.において、計算の都合上座標値を移動しているため、これを加えると次のようになる。 +ゾウの表面積を求める公式は以下の通りです。 ゾウの表面積の求め方 45 ( 6807 × 身長 ) ( 7073 × 前足の太さ ) なんでこんな式になるんでしょうか? 特に最初の45は一体何なのか鼻? さっぱり分かりませんが、とにかくこれが公式だそうです
1月公開! 算数「角度と面積の公式」学習ポスター&クイズテスト 小学生学習ポスターとそれに関するテストを毎月公開していくコーナーです。 1月は「角度と面積の公式」学習ポスター&クイズテスト(高学年用・低学年用)を公開します!1公式」「12分の1公式」「3分の1公式」と呼ばれている式を紹介する。 1 6分の1公式 下の図のように,放物線と直線,あるいは放物線同士で囲まれた部分の面積を求めるときに使用 する公式である。 S因長方形的面積為 ,從而橢圓的面積是 。 我們也可以考慮高維數類似測度,比如可能想要求出球體的體積。當我們知道球面面積公式後,可以使用與圓一樣的「洋蔥」積分法。 參見 圓、圓周率
フリスの伝達公式 Technical Report YK040 Jan 10, Y Karasawa 4 長さlの微小ダイポールアンテナ(以下、微小ダイポールと呼ぶ)を角度 (ダイポール方 向を =0)方向から到来する平面波(電界の強さE r)内に置き、その受信電力からアンテナ 利得や実効面積を以下の手順で求める。面積:物體的表面—平面圖形的大小。 體積:物質或物體所占空间的大小或占據一特定容積的物質的量。 計算公式 面積 長方形面積=長×寬 = 正方形面積=邊長 2 = 平行四邊形面積=底×高;菱形面積公式 1菱形面積公式就是由三角形面積公式得來的。 菱形面積=兩個三角形面積的和 2 對角線乘積的一半,即S=(兩對角線相乘)X1/2 (只要是對角線互相垂直的 四邊形 都可用,如正方形,菱形,記為:二分之一對角線相乘)。 3 S菱形=底×高 (跟




图形面积周长公式第1页 驾考预约大全



平行四边形的面积公式 聚热点网
楕円の面積公式について a = b a=b a = b の場合,曲線の方程式は x 2 y 2 = a 2 x^2y^2=a^2 x 2 y 2 = a 2 となり,半径 a a a の円を表します。よって,面積は π ⋅ a ⋅ a \pi \cdot a\cdot a π ⋅ a ⋅ a となり楕円の面積公式は確かに正しいです。つまり,楕円の面積公式は面積(英語: Area )是用作表示一個曲面或平面 圖形所佔範圍的量,可看成是長度(一維度量)及體積(三維度量)的二維類比。 對三維立體圖形而言,圖形的邊界的面積稱為表面積。 計算各基本平面圖形面積及基本立體圖形的表面積公式早已為古希臘及古中國 人所熟知。四角形の面積 ・正方形の面積 1辺の長さから正方形の面積を計算します。 ・長方形の面積 縦と横の長さから長方形の面積を計算します。 ・台形の面積 上底と下底、高さから台形の面積を公式を使って計



三角锥形面积公式三角形的体积公式是什么 银颜网




圓的面積公式圓的面積公式 高三網 Qqkaii
正方形の面積を求める2つの公式 具体例で学ぶ数学 > 図形 > 正方形の面積を求める2つの公式 最終更新日 ~公式その1~ 1辺の長さが分かっている正方形の面積は (1辺)× (1辺) または (たて)× (よこ) で求めることができる。 ~公式その2~です. 南海 これの根拠となった面積の式は? 耕一 です. 南海 この角 は大きさを表すのだが,これを oaからobへの符号つきの角とし,左回りを正としよう. つまり3点o,a,bが反時計回りに廻っているとき, の面積を正とし,逆回りのとき負とする. このとき上の絶対値はどのようにはずす它的面積是多少平方厘米? 步驟(1) 選擇公式 圓的面積 = πr2 步驟(2) 代入公式 = 314 × 42 步驟(3) 計算過程(不能跳步) = 314 × 16 步驟(4) 注意單位 = 5024(平方厘米) 步驟(5) 列出答句 答:它的面積是5024平方厘米。 二、計算題。
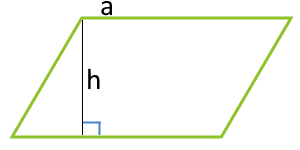



平行四邊形的面積
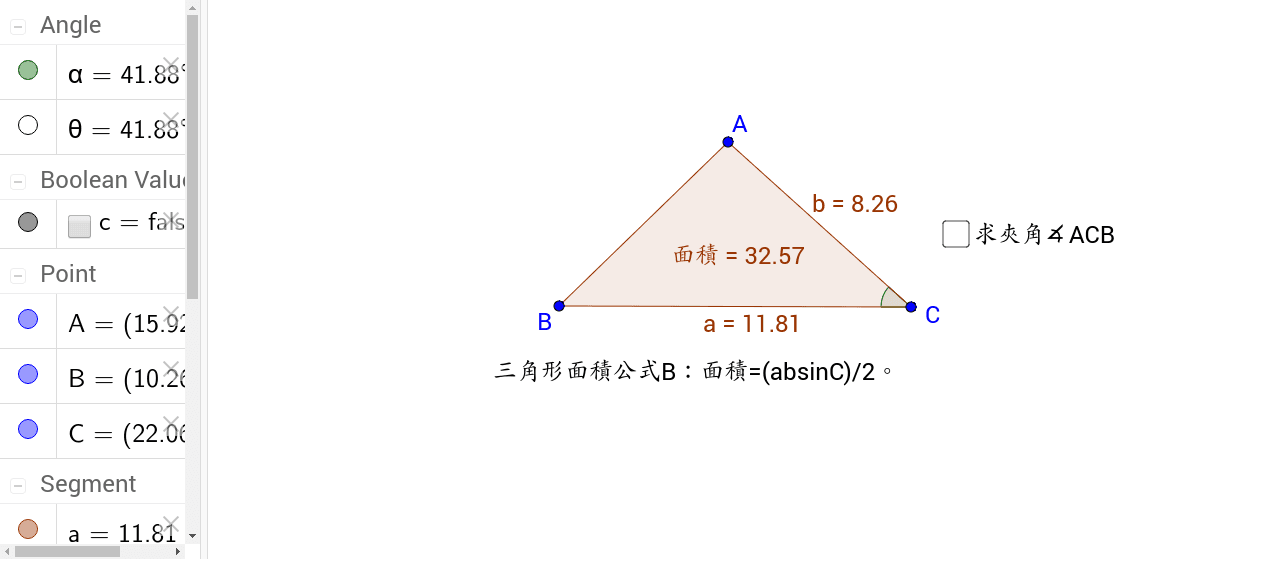



三角形面積公式b2 Geogebra
立方体の表面積の公式 立方体の表面積の公式は、底面積と側面積の合計です。立方体は全ての辺が同じ長さです。立方体の面は6面あります。よって 立方体の表面積の公式=6a 2 です。aは立方体の辺の長さです。下記もご覧ください。三角形の面積(3辺からヘロンの公式) 三角形の面積(1辺と2角から) 正方形の面積 長方形の面積 台形の面積 台形の高さ・面積(4辺の長さから) 台形の1辺・面積(3辺の長さと高さから) ひし形の面積 平行四辺形の面積(底辺と高さから)四邊形的面積 蔡聰明 一 問題的提出 給一個三角形, 已知三邊長, 那麼它的 面積可用著名的 Heron 公式來求算。 這我們 在"談Heron 公式 記一段教學經驗"一文 中, 己經有所敘述1。 現在要加以推廣, 我們 自然想到了兩個方向 (i) 維數的提高, 從平



三角形面积公式 玄数
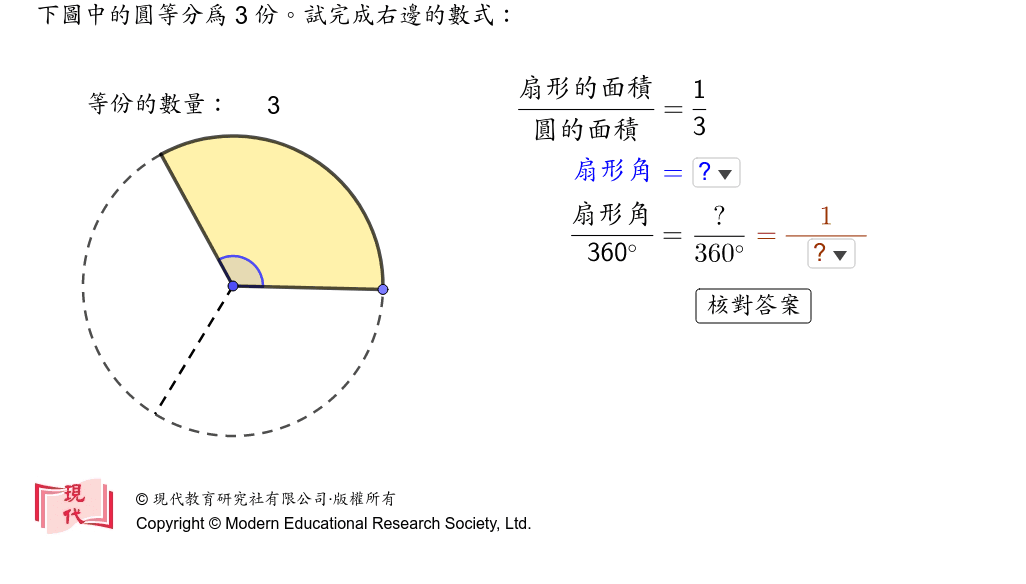



扇形面積公式 Geogebra
椭圆面积公式 : S=πab 椭圆面积定理:椭圆的面积等于圆周率(π)乘该椭圆长半轴长(a)与短半轴长(b)的乘积。 椭圆面积公式 应用实例 椭圆的长半轴为8cm,短半轴为6cm,假设π=314,求该椭圆的面积。 答:S=πab=314*8*6=(cm²)V = 体積 (角錐台) S1 = 角錐底面積 S2 = 角錐上面積 球体 V = 体積 A = 球体の表面積 r = 球体半径 楕円体 楕円体の体積 → 楕円体 楕円体の表面積 台形 A = 面積 A = 面積 ヘロンの公式 A = 面積 = bh/2 又は ヘロンの公式 jin 球の表面積の求め方の公式を1発でおぼえる方法 球の表面積の求め方の公式である、 4×π×半径の二乗 を一発で暗記してできちゃう語呂を紹介しよう。 このイメージさえ掴んじまえば、テストでも公式を忘れないはず! 球の表面積の公式を暗記するための
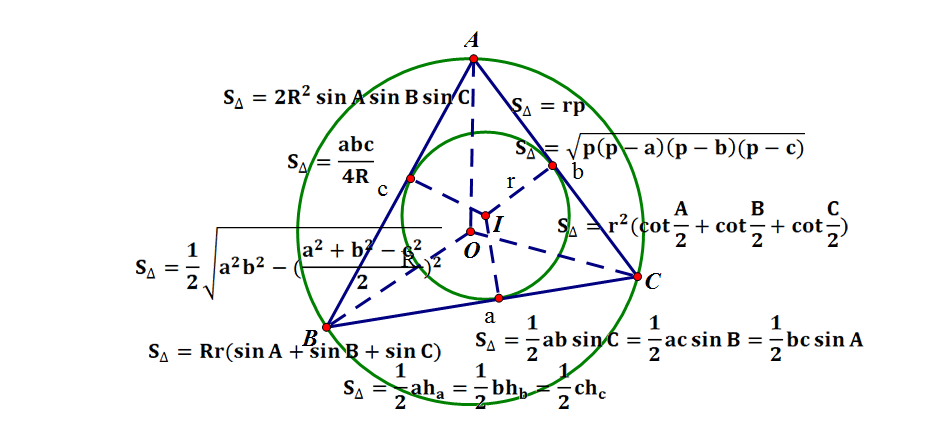



从三角形的面积公式谈起 知乎




三角形的几个面积公式都是什么时候发现的 网易订阅
相關詞條 面積公式 面積公式,其中包括長方形面積公式、正方形面積公式、扇形面積公式,圓形面積公式,弓形面積公式,菱形面積公式,三角形面積公式,梯形面積公式等多種圖形的面積公式。 圓面積公式 圓面積公式是一種定理定律。為圓周率*半徑的平方,用字母可以表示為S=πr²或S=π*(d/2)²。ひし形の面積を求める公式は $$(対角線)\\times (対角線)\\div 2$$ となっています。 &nbsAbout Press Copyright Contact us Creators Advertise Developers Terms Privacy Policy & Safety How works Test new features Press Copyright Contact us Creators




C语言中利用三条边求得三角形的面积公式 海伦公式 Phoenix为梦而战的博客 程序员宅基地 C语言海伦公式 程序员宅基地



梯形面积公式 用2种拼组 2种分割 1种割补法
東大塾長の山田です。このページでは、「積分の面積公式」について解説します。積分で面積を求める有名な公式「1 / 6公式」,その他にも,曲線と接線の間の面積を求める「1 / 3公式」,「1 / 12公式」についても詳しく解説しているので,ぜひ勉強の参考にしてください!




多边形面积 Segmentfault 思否



椭圆面积计算公式 椭圆面积计算公式画法




面积问题 小奥的孩子也看过来吧 秒杀初中生 每日头条
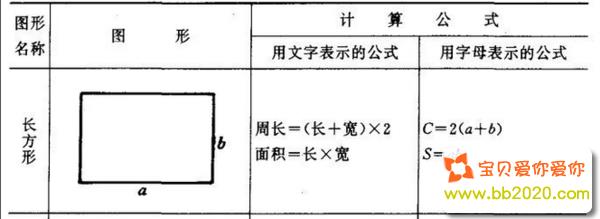



长方形的面积公式是什么 怎样推导的出来的 图解 小学资料 手机版



侧面积公式是什么 万图壁纸网




弓形面積公式弓形面積計算器 Qwvatk



平行四边形面积公式 平行四边形的面积计算公式 篆体字转换器



Q Tbn And9gcs4mf4ga4ivcw9oaofx1 Zkqgkhy6m1tx85ng7ya0kcksl0rfiq Usqp Cau
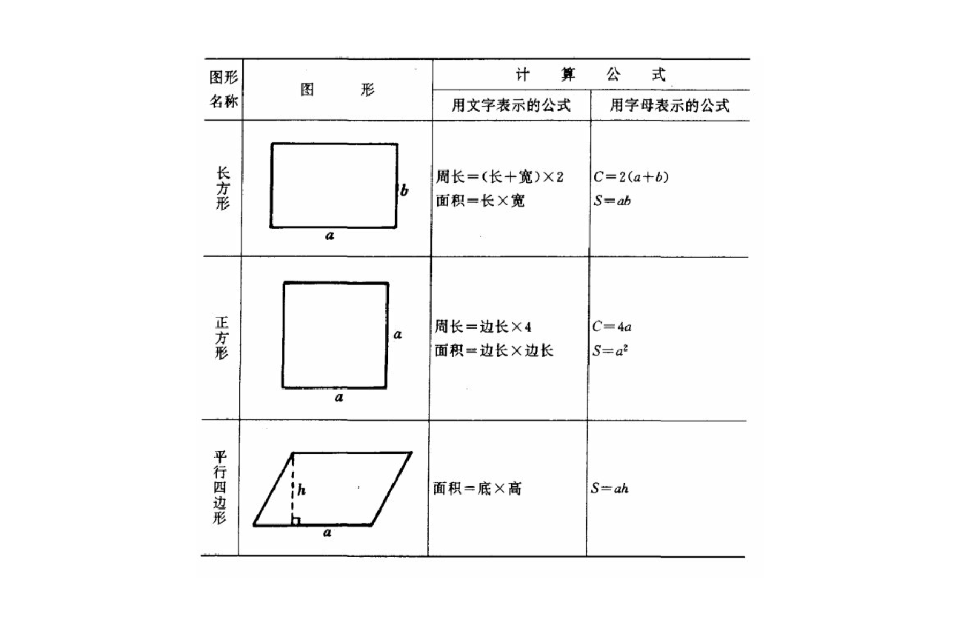



面積公式 常見面積定理 圓公式 扇形公式 圓環面積 三角形公式 海倫公式 坐標公式 中文百科全書



1



什么 任意四边形也有面积公式 海伦公式的推广及讨论 哔哩哔哩 Bilibili



面积公式小学数学 万图壁纸网
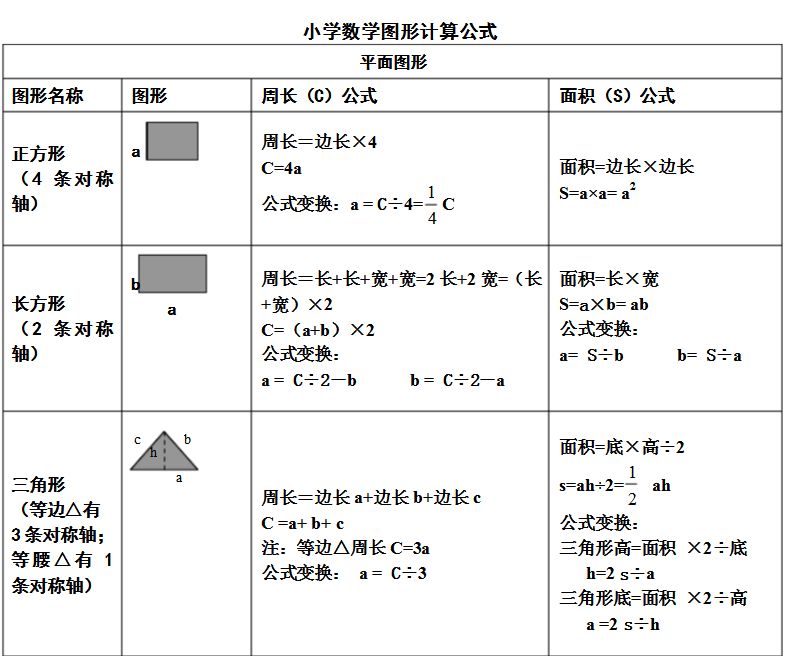



图形面积的计算公式 Csdn



平行四边形的面积公式是什么




常用圖形求面積計算公式 人人焦點



圆面积公式大全 三角形面积计算公式大全及练习题 尚书坊



面积公式大全图片 搜狗图片搜索




周长面积公式



体积公式面积公式 作业 慧海网



1



小学数学图形的周长 面积 体积公式 孩子学习必备 周长 体积 圆柱 新浪新闻




三角形的面積



面积公式 搜狗百科




股票一个区域画阴影公式 数学几何阴影面积公式 天空财经



三角形面积公式 快懂百科




正方形面积公式 正方形面积公式对角线 环球信息网



梯形面积计算公式 梯形面积计算公式画法




三角形的面积公式小学



1




不平行四边形面积计算公式与在线计算器 三贝计算网 23bei Com



棱柱的侧面积公式直棱柱的侧面积 全面积怎么求 麦税尼网



六年级扇形面积和弧长公式 初三网




三角形正多边形面积公式 三角形png图片素材免费下载 图片编号 Png素材网




扇形面積公式 公式 推導過程 注意事項 中文百科全書
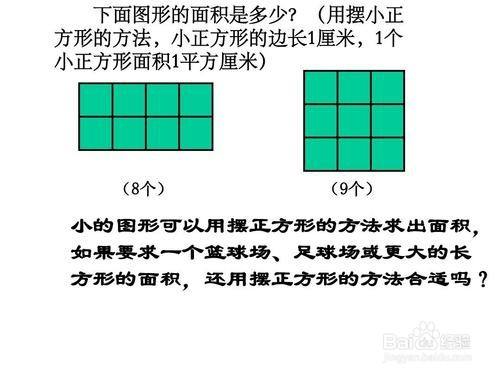



长方形的面积公式是怎么得到的 百度经验



图文版 小学数学图形的周长 面积 体积公式 小学 香蕉教育网
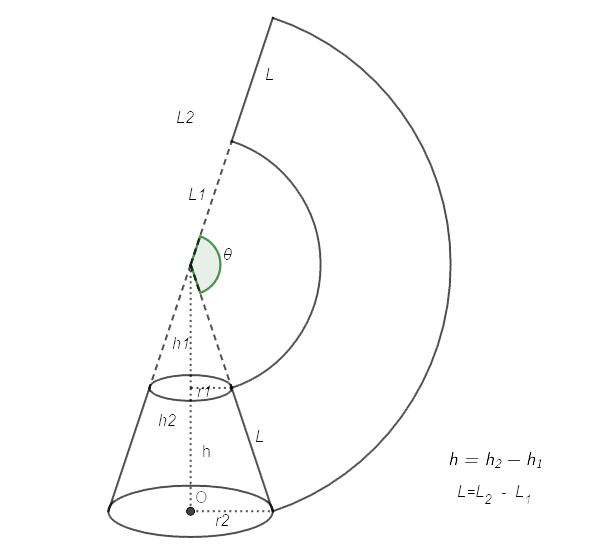



圆台侧面积和体积计算公式推导 冰雪 悦灵 博客园




例題 長方形面積公式的應用 數學 均一教育平台
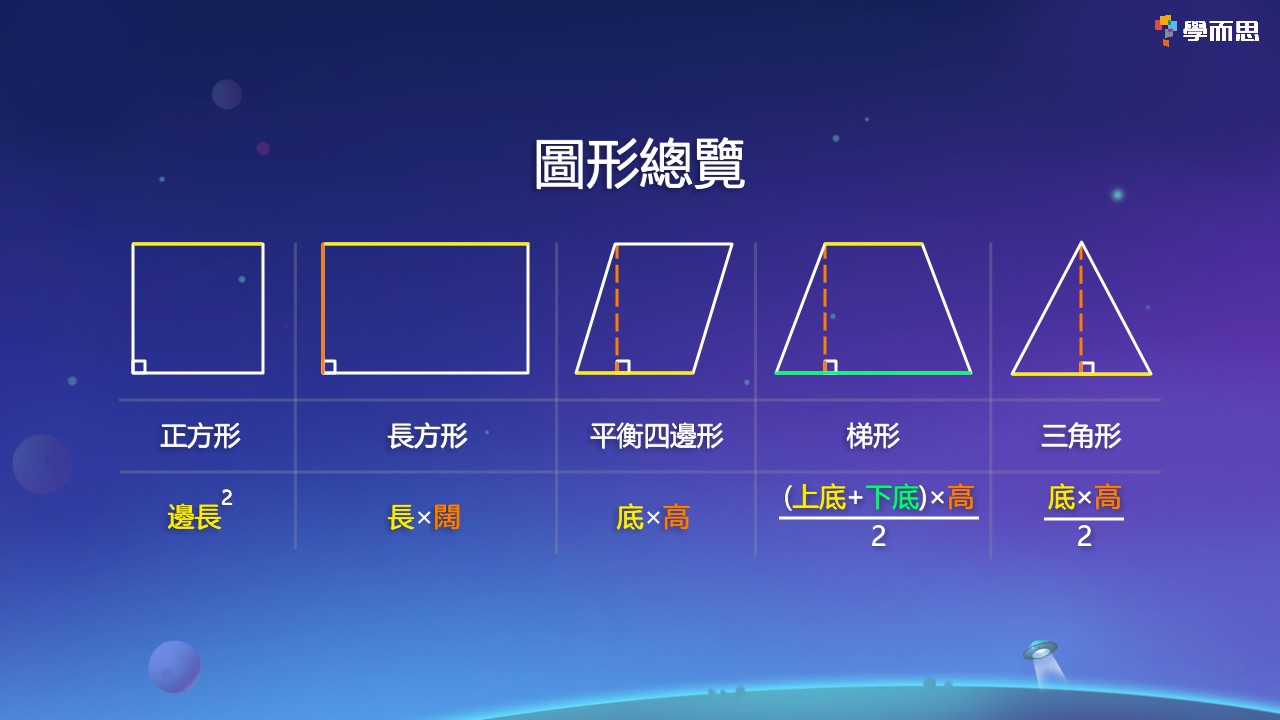



呈分試數學科必睇 圖形題目重點溫習攻略 公式 題目 學而思香港



圆面积的计算公式 圆的面积公式是怎么得到的 图文 叽叽歪歪吧




圆弧面积计算公式图解 百度经验



三角形面积公式 腾讯视频



斜三角形面积公式 西瓜视频搜索




长方体的面积公式第1页 驾考预约大全



面积公式 信息图文欣赏 信息村 K0w0m Com




5下面積概念題2 6菱形面積 Avi Youtube



圆锥的底面积公式是什么圆锥的底面积公式是什么 朵拉利品网



梯形面积公式 用2种拼组 2种分割 1种割补法




Amc 10 第一讲 数学中的面积公式都是怎么来的 知乎



梯形面积公式求下底 不规则求梯形面积公式求不规则梯形的面积的公式 尚书坊
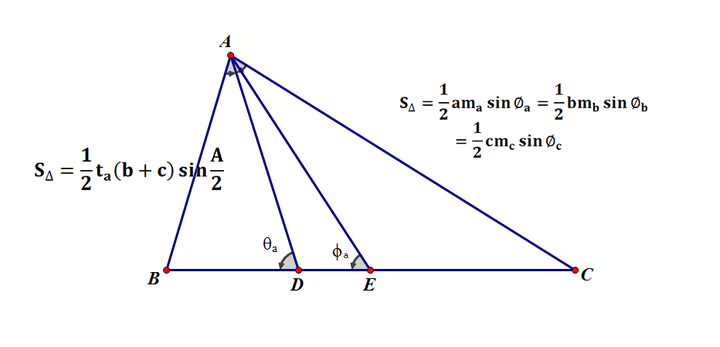



三角形的面积公式七叙 知乎




十七种三角形面积公式




十大家装公司 梯形面积公式 梯形面积怎么计算 合抱木装修网




常用求面积 体积计算公式 豆知网




直角三角形的面积公式 三角形的面积怎么求 环球信息网




梯形面积计算公式
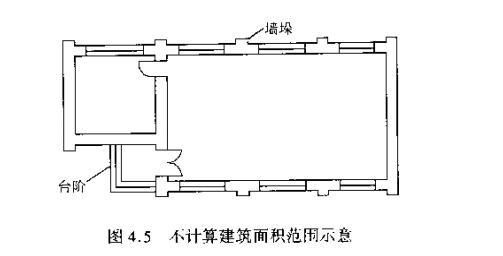



面积公式大全 面积公式大全小学 小学数学公式大全表




小學所有的數學 圖形的計算 公式 每日頭條



三角形面积公式余弦定理 快懂生活



用海伦公式求三角形面积 只知三角形三条边分别是3 5 6 如何求三角形面积 哔哩哔哩 Bilibili




圆的面积公式的应用教学反思 育儿科普 靓范儿




梯形面积公式是什么梯形面积怎么计算 传承网




数单位正方形求面积计算公式 视频 长方形 正方形面积的计算 可汗学院



梯形面积公式 用2种拼组 2种分割 1种割补法



扇形面积公式带图 万图壁纸网



半圆周长和面积的计算公式 学习岛



心形线面积计算为什么是a 2 1 2r 2dv18 心形线面积公式推导 崇爱网



锥形面积公式怎么计算圆锥的面积 用什么公式 朵拉利品网
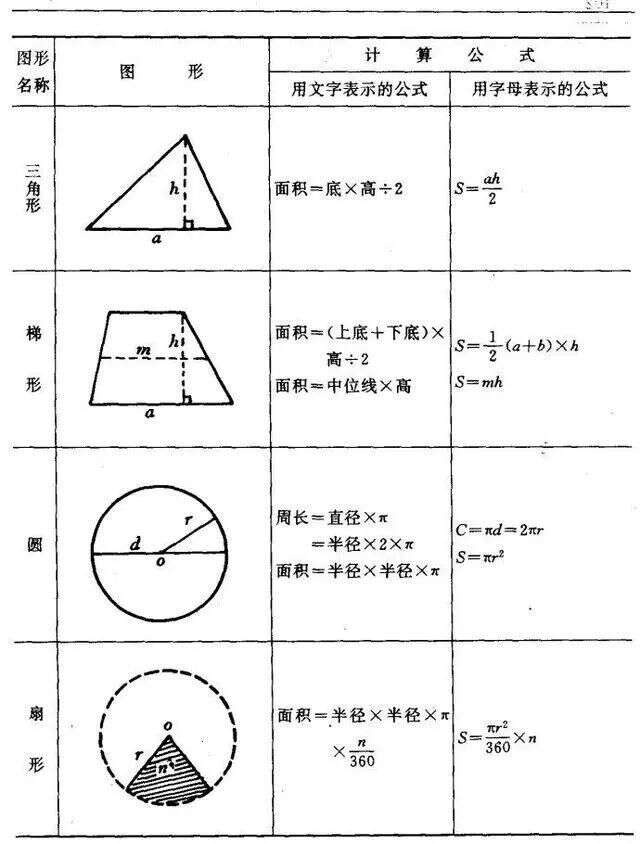



小学数学图形的周长 面积 体积公式 孩子学习必备 楠木轩



数理之路 三角形面积公式以及三角函数正弦和角公式 腾讯新闻



小学数学公式 菱形面积公式 数学公式 奥数网



三角形面积计算公式 三角形面积公式 越多越好 100查分网



小学生五年级面积公式 西瓜视频搜索
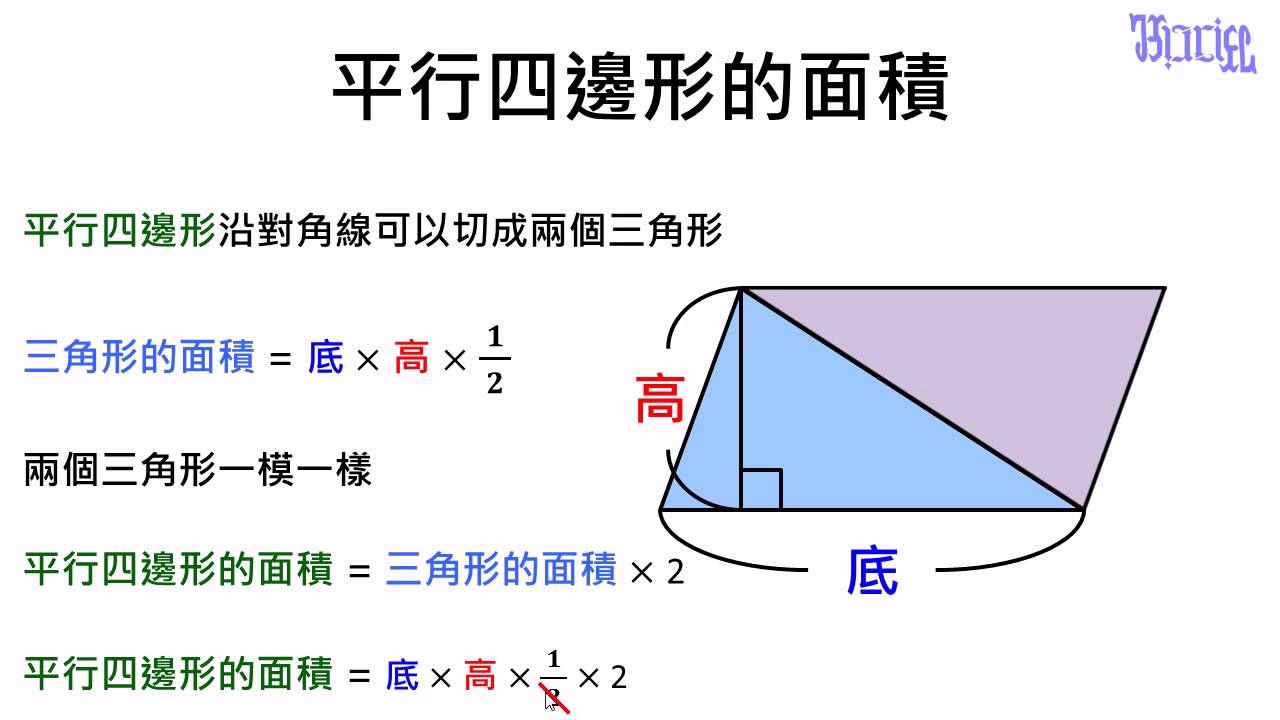



面積 04 平行四邊形的面積計算方式證明1 Youtube




面积公式 搜狗百科



四边形面积公式 面积最大值问题 哔哩哔哩 Bilibili
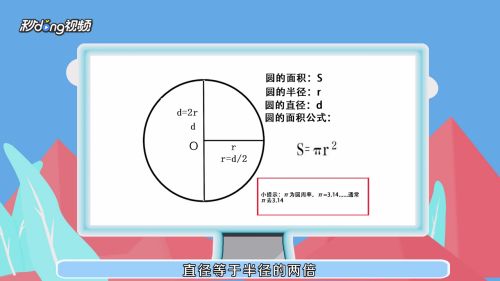



圆的面积公式怎么算 百度经验



7 4 平行四邊形的面積公式 高市資教中心教材網




三角形面积公式 三角形面积万能公式 十安知识网




三角形公式面積三角形面積公式 Utvos



等边三角形面积公式表 等边三角形面积计算 七月seo




小学数学图形面积公式 小学阶段 图形求面积 的10大方法 三好网



梯形面积公式换算 梯形形面积计算公式梯形形的面积公式三角形梯形面积公式 尚书坊



掌握椭圆中焦点三角形面积公式 解题速度提高一倍 简书



图文版 小学数学图形的周长 面积 体积公式 圆柱
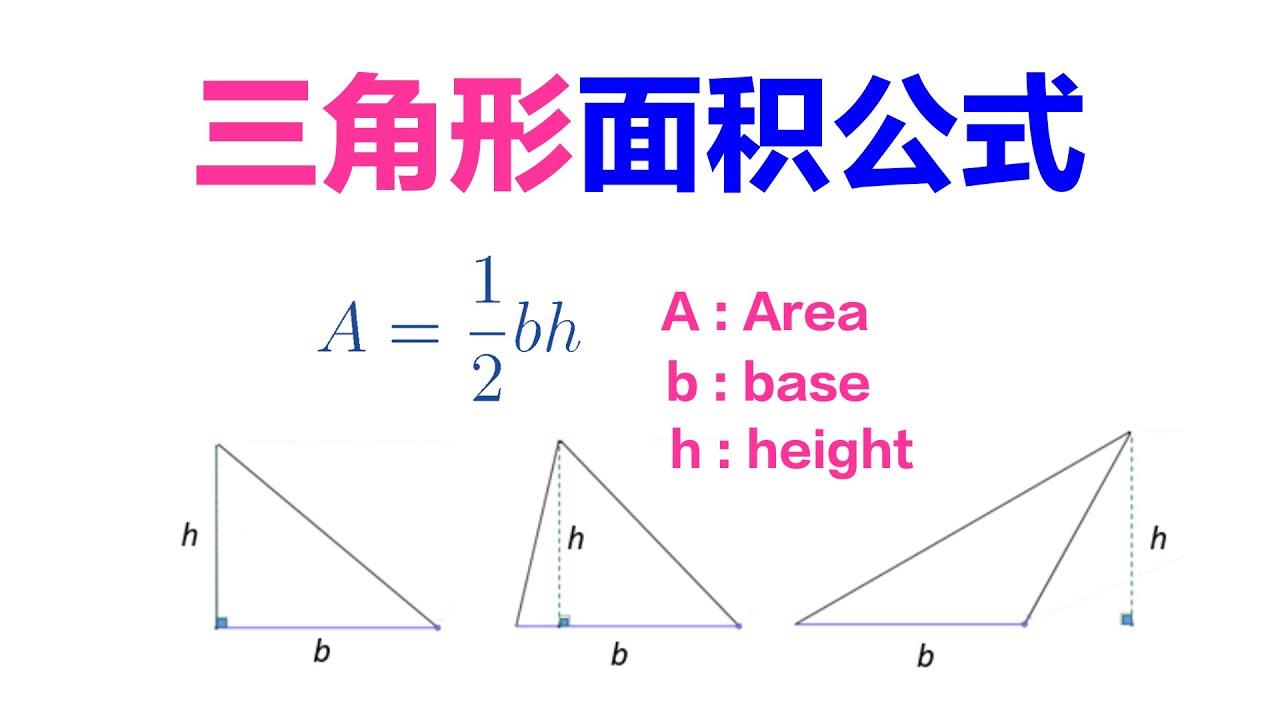



三角形面积公式的证明 Youtube




圆的面积公式 圆的面积公式是什么 517鲜花




三角形面积公式 三角形面积公式盘点 52fmz购物网



圓公式面積 觀念 圓面積計算公式的推導 Eyflka



面积公式 快懂百科



梯形体积公式梯形体积公式 一加一




08 長方形面積公式的應用 Youtube



0 件のコメント:
コメントを投稿